#44 - Peeling the onion, market snapshot and much more!
⚔️ LNM Fam
🏆 Degen Award goes to @Trigger_jw for his based trading strategy:
Speaking of trading strats, we have made a Python Bot inspired by the great work of @citlayik, @JohnOnChain and many others!


This is just the beginning, feel free to add your ideas and strats to reach the moon! One small satoshi for man…

🏆 He’s back! @tonybitcorn displays yet another example of his skills to grab this week’s meme award:
📊 Market snapshot
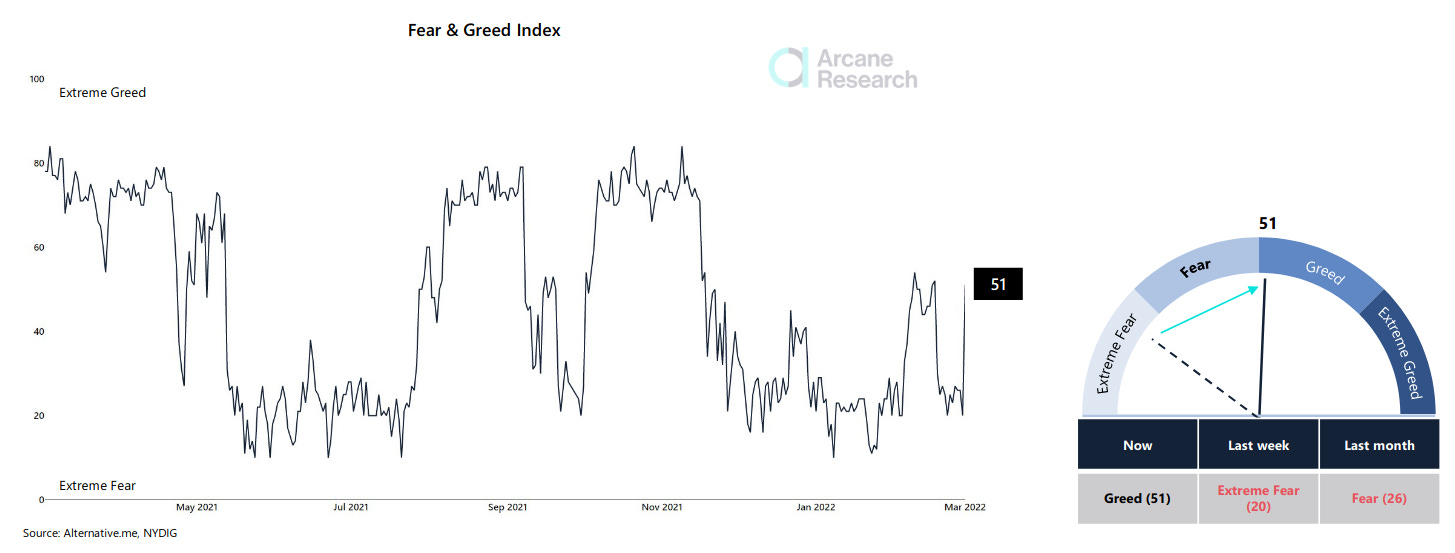
Fear and greed index back to neutral
The Fear and Greed Index suddenly entered neutral territory after staying in the "extreme fear" area for most of 2022. One of the reasons the crypto market remained in a prolonged fearful state was geopolitical uncertainty related to the imminent Russian invasion of Ukraine.
As the attack unfolds, investors seem to have changed their opinions on how increased geopolitical uncertainty and conflicts may affect the crypto market.
Highest daily bitcoin trading volume since December
The real bitcoin trading volume (which includes Bitwise 10 exchanges, LMAX, FTX) pushed above $10 billion last Thursday when Russia invaded Ukraine. This was the highest volume seen since December 4th, and Monday also saw high trading volumes.
The market seems to be waking up after a dozy February.
Bitcoin’s largest daily percentage gain in one year
On Monday, the bitcoin price increased 14.5%. This daily price increase was the largest since February 8th, 2021, when Elon Musk announced that Tesla had bought $1.5 billion in bitcoin. It made the 7-day volatility shoot up to 5.4%, which is the highest level since June 2021.
Once again proving that bitcoin often behaves opposite of the rest of the financial markets concerning volatility, as upwards price movements often cause the most significant volatility spikes.
Basis reaches all-time low on Binance’s quarterly BTC futures
The 3mth annualized futures basis on Binance reached its lowest 24hr average level in history on Monday of 1.17%.
The futures basis on Binance reached a new all-time low on Monday, plummeting to levels lower than the July 21st lows. The previous low coincided with BTC bottoming after its sustained summer sell-off and was followed by a substantial short squeeze as BTC broke out of its then $30k to $40k range, analogous to a range of $35k to $45k today.
While history doesn’t necessarily repeat, and the basis overall has been far more muted since May, the basis reaching historical lows reflects that the sentiment is poor and possibly that sellers are losing fire powder.
Perp traders not convinced by recent rally - Funding rates still muted
Funding rates in its third consecutive month in a neutral to below neutral regime.
Funding rates remain in neutral to below neutral terrain. Thus, despite the strong recovery yesterday, perp traders remain cautious.
We’ve now seen three consecutive months of a neutral to negative funding rate regime, similar to what we saw during the summer bear market of 2021.
Liquidations has picked up in the last week, with Feb 24th and Feb 28th seeing the largest daily short liquidation volume in bitcoin since the volatile Dec 4th crash.
Despite yesterday’s liquidation uptick, the perp open interest remained fairly stable, falling from 223,000 BTC to 219,000 BTC, suggesting that traders are actively re-adjusting risk.
👉 This week Arcane Research gives free access to the premium version of our report. Enjoy this special edition.
🤔 Peeling the Onion - Part 3
This article is the third concerning Onion Routing. Therefore, it is recommended to read the first and second parts before this one.
TL;DR
The Onion Packet contains several, layered, encrypted Onion Payloads which indicates to each node the parameters of the HTLC (or PTLC) it must create to forward the payment. This includes the amount to forward, to who, as well as what expiration delta to maintain between HTLCs. In order to avoid using its node public key, the original sender of the payment uses a one-time session key, different for each hop in the route. The sender builds the payload and applies successive layers of encryption on said payload, using said keys. As the Onion Packets moves along the route, each node checks the integrity of the packet and extract its own payload, before sending it to next node in the route.
Which Keys does Onion Routing use?
The whole goal of Onion Routing is to hide who the sender and recipient of a payment are. Hence, when Alice sends a payment, she can’t just use her node’s public key to provide for the encryption and integrity of the Onion packet she constructs. Instead, Alice will use a one-time session public and private key for each hop in the route. The combination of this session key pair with the hop’s public key will allow here to generate a shared secret, which the aforementioned hop will also be able to compute simply by knowing Alice’s public session key (and, of course, its own private key). This way, the message intended for that hop can be encrypted so that only this node will be able to read it ; while at the same time the intermediary node will be able to tell that the data in the message has not been tampered with and was indeed put there by Alice (data integrity). Let’s see how this works!
Let’s share a secret
Alice starts by creating a session private key for this payment and the associated public key, thus not revealing her node’s public key. She sends the public session key in clear to Bob in the Onion Packet, so that both of them can compute an identical shared secret. In what follows, we will denote Alice’s session private key as a and the corresponding public key as A = a*G, where G is the generator point on the elliptic curve, which we introduced in this article about PTLCs. On the other hand, B will be Bob’s node public key, with b being the associated private key.
Alice can compute a secret
s = a*B, because she knowsa(which she just generated) andB(it’s Bob’s node public key, so this data is available to all, and especially to Alice who chose to route her payment through this node).Bob can compute a secret
s' = b*A, because he knowsb(it’s his own node’s private key) andA(Alice’s session public key, which she just sent to him in the Onion Packet).
Now, what if I told you that s and s' are actually the same? Indeed, if we use some parentheses to highlight the breakdown of public keys into private keys times G, as well as some interesting properties of elliptic curves multiplication, we can see that:
s = a*B = a*(b*G) = (a*b)*G = (b*a)*G = b*(a*G) = b*A = s'
We just demonstrated that s and s' are equal. We will therefore call them the shared secret between Alice and Bob, denoted ss.
That was for Bob, the first hop on the route. Now, Alice needs to do the same for each hop. Moreover, she needs to do it with a different session key for each hop, or else it could be easier for an attacker to deanonymize her. One simple, naive way of doing so would be by generating a distinct session key for each hop and sending each hop the key it is concerned with in its Onion Payload. But this would increase the size of the Onion more than necessary, and the people who designed the Onion Routing protocol in use in the Lightning Network [1] actually came up with a much smarter way.
Once Alice has generated a session key for the first hop (Bob), she will deterministically alter it for the other nodes so that each hop has a different session key. To do so, she uses this simple formula:
session_key_i = session_key_{i-1} * SHA-256(node_pubkey_{i-1} || shared_secret_{i-1})
where || means a concatenation.
So the message Alice sends to Bob looks something like this:
|Version|Session Key|Onion Payload|Checksum|
We’ll soon cover into more details how Bob verifies the checksum and decrypts the Onion payload, but let’s look at the session key first. With it, Bob can generate the shared secret on his end simply by performing an elliptic curve multiplication of the session key SK (caps because it is a public key) with his own private key:
ss = b * SK
With this shared secret, he is now able to derive some keys that will be useful for him to check the integrity of the payload (checksum), as well as decipher it to access the data addressed to him, as we’ll see in the next section.
Once Bob has read his part in the Onion Payload, he removes it and adds some filler at the end of the payload so that it still weights the same as before (1300 bytes). Then, he computes a new session key for Carol, with the formula we saw earlier:
session_key_carol = session_key_bob * SHA-256(node_pubkey_bob || shared_secret_bob)
and appends this new session key before the Onion. From the part of the payload he deciphered and removed, Bob also extracts a checksum for Carol, which he puts after the payload. He then adds the version byte at the beginning and, tada!, Carol’s message is ready to be sent:
|Version|Session Key Carol|Onion Payload|Checksum|
This way, Carol receives from Bob a message with exactly the same structure as the one Bob received from Alice. Therefore, she can’t tell whether Bob was the emitter of just an intermediary node. Conversely, when Bob received the first message from Alice, he couldn’t tell whether she was a hop in the route or indeed the sender of the payment.
Each hop along the route repeats the same process, until the message reaches the final node:
Generate shared secret from the multiplication of the session key with their own private key.
Derive various keys from shared secret to:
check integrity
decypher the Onion Payload
Extract from the Onion Payload the part that is readable to them. The rest isn’t intelligible because it is encrypted with the public keys of other nodes.
Add some filler in replacement so that the Onion Payload still weights the same.
Extract the checksum for the next hop from their own part of the payload (which they just extracted in step 3) and append it after the Onion Payload.
Compute the session key for the next hop by applying the formula to their own session key, public key and share secret. Append this new session key before the Onion Payload.
Add the version number (just
0for now) before the rest.Send this new message to the next hop.
And derive some keys
We’ve seen in what precedes how each hop in the route is able to generate a shared secret, which besides themselves is only known to Alice. Each node in the route will then use this shared secret to derive 4 different keys:
rho used for the encrypting of the Onion Payload,
mu used for the integrity verification (checksum),
um used for error reporting (more on that later),
pad used by Alice in the beginning to generate initial padding.
One crucial aspect of this key generation is that, for each hop, Alice and the hop are able to generate the same keys, but anyone else just can’t. This is because only Alice and the hop can generate the same shared secret (Alice with the private session key corresponding to this hop and the hop’s public key ; the hop with the public session key and its own private key).
We saw in the beginning of this article how Alice builds the Onion Payload. It is now time to see how she does so while also adding several layers of encryption.
Alice starts by generating 1,300 bytes of random data (using the pad key), represented as Fs (stands for filler). That’s her Onion Payload at the beginning.
|FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF|
She takes the last hop payload (eg the payload of the recipient Eve), and adds 32 bytes of 0s at the end of it. Those 0s act as the “checksum” over Eve’s payload, and it being all zeroes indicates to Eve that she is indeed the final node in the route.
She adds Eve’s payload and its checksum to the left end of the Onion Payload and remove the same amount of filler from the right end, so that the Onion Payload still has a length of 1,300 bytes at all time.
|PayloadECheckFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF|
Alice uses the rho_eve key [2] and a specific algorithm to generate a 1,300 bytes stream. What is important to note at this point is that anyone with the same key and using the same algorithm would generate the exact same 1,300 bytes. Then, Alice applies the XOR operation between the Onion Payload and the bytes generated with the rho_eve key. There is no need to know what XOR does exactly, apart from the fact that this function has the nice property that, if applied twice on an object, it returns the object itself ; but if applied once, it returns something completely different (it’s bit like a light switch). After the XOR operation, the whole Onion Payload looks like some random byte stream.
|ac7f98b6eec079f9e2d9c9d243255f40e25ba26107ee8dff3d97c5b2d88f13d3f|
Alice uses the mu_eve key to compute the checksum of the whole Onion Payload.
Alice then takes Daniel’s payload, put it with the checksum she just computed (step 5) and append all of it at the left end of the Onion Payload. Just like in step 3, she also removes the same amount of data from the filler (right end of the Onion Payload) that she just added, so that the Onion Payload still is 1,300 bytes long.
|PayloadDCheckac7f98b6eec079f9e2d9c9d243255f40e25ba26107ee8dff3d97|
Then, she obfuscates the Onion Payload as she did in step 4, but this time using the rho_daniel key she shares with Daniel.
|4bcf430964f7b4156aca1b1321f77a61c5af86dbf5876a2b320287e007a70bf2a|
Using the mu_daniel key, she computes the checksum of the whole Onion Payload.
Alice then takes Carol’s payload and the checksum she generated in step 8, and add them at the left end of the Onion Payload. Once again, she removes the excess filler from the right side of the Onion Payload so that it still measures 1,300 bytes.
|PayloadCCheck4bcf430964f7b4156aca1b1321f77a61c5af86dbf5876a2b3202|
Then, she encrypts the whole Onion Payload using the rho_carol key.
|afbe2be5df68754ae81c8c4a1ea83791b72a60a4f1ae26c7bc9e999cc31e267e2|
Like in step 8, she computes the checksum over the whole Onion Payload, this time using the key she shares with Carol mu_carol.
She appends Bob’s payload followed by the checksum to the left of the Onion Payload, and trims the excess filler from the right side.
|PayloadBCheckafbe2be5df68754ae81c8c4a1ea83791b72a60a4f1ae26c7bc9e|
She encrypts the whole Onion Payload using the rho_bob key she shares with Bob.
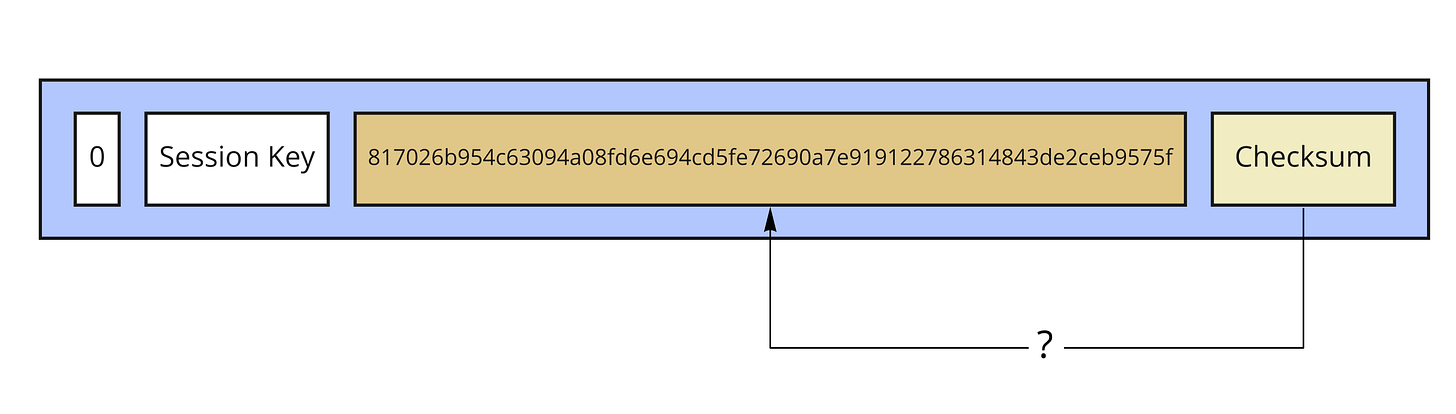
|817026b954c63094a08fd6e694cd5fe72690a7e919122786314843de2ceb9575f|
With mu_bob, she computes the checksum over the whole Onion Payload. She puts it after (right side) the Onion Payload.
|817026b954c63094a08fd6e694cd5fe72690a7e919122786314843de2ceb9575f|Checksum|
Now, all Alice has to do is add the version byte and the session key before (left side) the Onion Payload, to conclude the Onion Packet.
|0|Session Key|817026b954c63094a08fd6e694cd5fe72690a7e919122786314843de2ceb9575f|Checksum|
The Onion Packet is ready to be sent to Bob! 🥳
Peeling the Onion
Now, the nodes in the route will receive the Onion Packet from the node before them, extract their own payload plus the next hop’s checksum from it, add some deterministic filler so that the Onion Payload still weights the same after they removed their part, replace the checksum at the end of the Packet with the one they just extracted, and pass the Onion Packet along. Let’s see in more details what happens sequentially:
Bob receives the Onion Packet from Alice. The first thing he does is check the checksum against the whole, still encrypted, Onion Payload.
If the check is successful (meaning the data hasn’t been altered), he decrypts the Onion Payload. To do so:
he generates a 1,300 bytes stream with the rho_bob key and the same algorithm that Alice used. Hence, he obtains the same 1,300 bytes as Alice in step 13.
he applies the XOR operation between the 1,300 bytes he generated and the Onion Payload. As stated before, applying XOR twice is like doing nothing. Hence, after using XOR, Bob obtains the Onion Payload as it was before Alice herself used XOR on it in step 13. In other words, he decrypted his payload!
|PayloadBCheckafbe2be5df68754ae81c8c4a1ea83791b72a60a4f1ae26c7bc9e|
Bob extracts his payload
PayloadBand the checksumCheckfrom the Onion Payload. The rest of the payload is still encrypted. ReadingPayloadB, Bob knows what amount to transfer in a conditionnal payment, to whom, and with what expiry date.Now that Bob has extracted
PayloadBandCheck, the Onion Payload is shorter. To fix this, Bob uses a padding_key he derives from the pad key to generate enough filler at the end. This allows him to generate the same filler as the one Alice created, and he hence obtains the same Onion Payload as Alice in step 10. This is necessary for the checksumCheckto still be valid, as it was computed for Carol’s whole encrypted payload [3]. Bob adds the checksum for Carol after the Onion Payload
|afbe2be5df68754ae81c8c4a1ea83791b72a60a4f1ae26c7bc9e999cc31e267e2|Check|
🚧 Note that this deterministic filler generation is still something I feel I don’t completely grasp. I may have made some mistake or oversimplification. For instance, my understanding of the specification goes again what is written in Mastering the Lightning Network by Antonopoulos, Osuntokun and Pickhardt, and I would doubt myself before doubting the three of them. The important part is that filler was generated to keep the length of the Onion Payload at 1,300 bytes, and the checksum is still valid for the next hop. 🚧
For the Onion Packet to be complete and for him to be able to send it to Carol, Bob must still add the version byte and the session key. The version is still set to
0. For the session key, Bob uses what we saw in “Let’s share a secret” to transform the session key he received from Alice into a new session key. Note that this process is deterministic, that’s how Alice herself generated the four session keys (one for each hop, incl. Eve) and the associated shared secret. Hence, with this “new” session key, Carol will indeed be able to generate the appropriate shared secret and therefore rho_carol, mu_carol, and so on.
Bob has now constructed the whole new Onion Packet and he can send it to Carol.
|0|Session Key Carol|afbe2be5df68754ae81c8c4a1ea83791b72a60a4f1ae26c7bc9e999cc31e267e2|Check|
Once Carol receives the Packet from Bob, she does the same things that he did in steps 1 to 5. She uses the session key to create her keys rho_carol and mu_carol, uses mu_carol to check the cheksum against the Onion Payload, uses rho_carol to decrypt the Onion Payload, extra her own payload from it, generate deterministic filler to replace what she extracted, add the checksum for Daniel at the end and compute Daniel’s session key.
Then, she sends the new Onion Packet to Daniel.
|0|Session Key Daniel|4bcf430964f7b4156aca1b1321f77a61c5af86dbf5876a2b320287e007a70bf2a|Check|
Once he receives the Packet from Carol, Daniel does the same things. He ends up with the following Onion Packet, ready to be sent to Eve.
|0|Session Key Eve|ac7f98b6eec079f9e2d9c9d243255f40e25ba26107ee8dff3d97c5b2d88f13d3f|Check|
Eve finally receives the Onion Packet from Daniel. She uses the session key to generate the various keys, checks the checksum, and decrypt the Onion Payload, which is now nothing but her own payload and filler. She reads in her payload the information about the payment.
That’s it, folks! Using outstanding cryptography and some smart ass optimizations (session key randomization for the win!), the Onion Packet was moved from Alice to Eve while retaining privacy at all time.
By Fanis Michalakis, Bitcoiner & Techno Padawan @LNMarkets
Resources
Chapter 10 of Mastering the Lightning Network
Footnotes
[1] It’s called SPHINX and was designed by George Danezis and Ian Goldberg. Here is their paper if you’re into it.
[2] rho_eve refers to the rho key derived from the shared secret between Alice and Eve. I’ll use the same notation for other keys and other nodes.
[3] Note that in sequential order, the padding actually happens before the decryption of the payload. More details can be found in Bolt 4 and in the implementations' code (LND here).
⚡ Bonus
🤮🤮
🧵 Great thread to fight the next anti-Bitcoin narrative

🥰 Our first 1k ❤️ meme, thank you!
🤝 Reach out on Twitter, Telegram and Discord to build the future of trading together!